EcoDrain Payback Calculation Challenge
Okay, so let's see if you know how to calculate what the payback period is on the EcoDrain product.
Don't attempt to do this if you're not versed in semi-complex math problems!!!!
Here are the figures I want you to use.
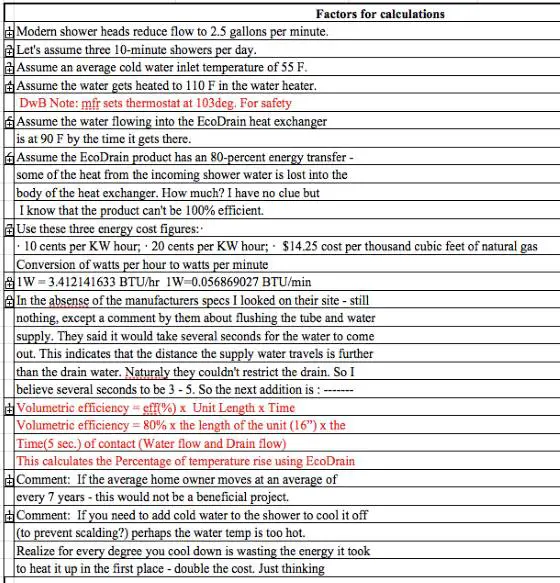
Modern shower heads reduce flow to 2.5 gallons per minute.
Let's assume three 10-minute showers per day.
Assume an average cold water inlet temperature of 55 F.
Assume the water gets heated to 110 F in the water heater.
Assume the water flowing into the EcoDrain heat exchanger is at 90 F by the time it gets there.
Assume the EcoDrain product has an 80-percent energy transfer - some of the heat from the incoming shower water is lost into the body of the heat exchanger. How much? I have no clue but I know that the product can't be 100% efficient.
Use these three energy cost figures:
- 10 cents per KW hour
- 20 cents per Kw hour
- $14.25 cost per thousand cubic feet of natural gas
You have to then calculate how many Btus of energy are harvested.
Now this is NOT EASY.
Why? Because only about 60 gallons of water will be heated up by the EcoDrain product. Remember the EcoDrain heats up the incoming water into the water heater. If you use 75 gallons of water in three showers, you probably only use about 60 gallons of hot water. The other 15 gallons is cold water used to temper the hot water so you don't get scalded.
With that number, you should be able to calculate how much LESS the average water heater has to work.
You need to know how many Btus of energy one might use to heat the 60 gallons of water that needs to be heated for the shower.
Is this starting to make sense?
Here's a clue. Years ago, I did a column about the tankless water heaters. To make a long story short, I demonstrated with my own gas bills that the average cost to heat water for a home is about $1 per day. This was using natural gas pricing from about fifteen years ago.
If you heat your water with natural gas, it's pretty easy to determine what you spend. You just look at your gas bills for May - September and average them. If you cook with gas in the summer, you'll have to deduct some of that cost for cooking. Same if you use gas to dry clothes. I believe you'll come up with the same number, about $1 per day currently.
If this is the case, THEN you know the EcoDrain product will probably only shave a few pennies off the cost to heat water since it's only salvaging heat from shower water and nothing else.
FINALLY, here's what you're trying to discover:
How long does it take to SAVE $600 in energy costs using the EcoDrain?
The actual product is listed on their website for $440.00 US Dollars. Let's assume a modest $160 installation cost by a pro.
Save all your calculations and show them long form to me so I can verify they're correct.
Send them to me at tim at ask the builder dot com.
AUTHOR UPDATE:
Today is October 2, 2014 and I received two submissions. One is from Dave Schwellinger who's an MBA chemical engineer. His calculations follow:
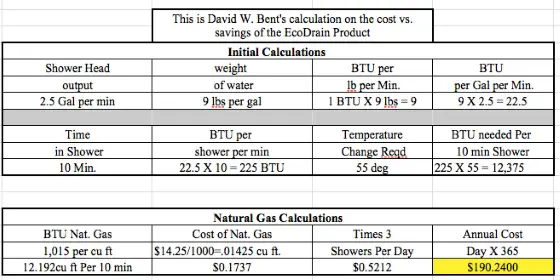
.
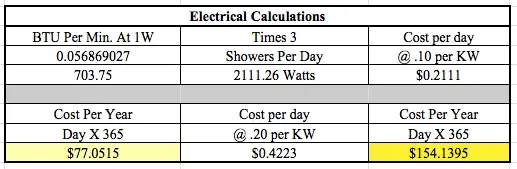
.
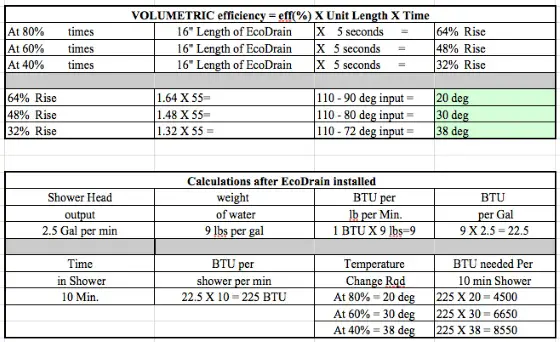
.
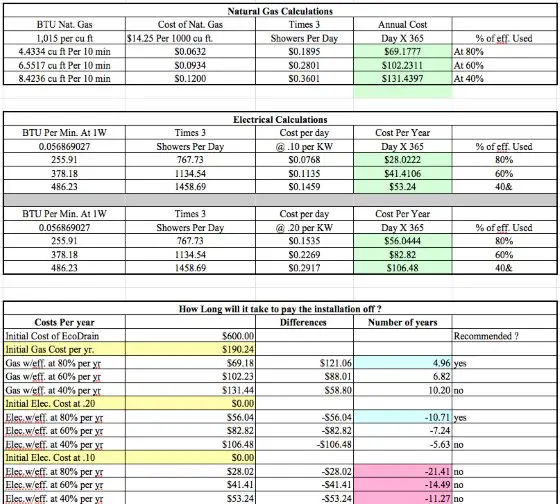
.
.
The crowdsouced calculations are wrong. We had offered our input and explanation of how calculations are done prior to this challenge. The problem with this post is that to someone who quickly glances at it, it has a air of credibility, it is calculated by an engineer who is also an MBA (so am I), on a authoritative site about building, and it uses terms like efficiency, btus and energy transferred. It looks legit even though it is just unchecked calculations by someone who is not a subject matter expert. If we were in university, this type of work would have to submitted to a professor who would review it. Few people get everything right the first time they attempt it and it would be abnormal to expect a 100% score on all assignments. In the real world, it seems you can get published on the internet on the first attempt with no review.
The engineer has correctly realized that energy from the drain water = energy in the makeup water. The basic equation for heating water is Q = m*Cp*dt, where Q is the energy required to heat water, m is the mass of water being heated, Cp is the specific heat of water, and dT is the temperature rise of the water being heated (Tout - Tin).
Qhot = mhot * Cp *(Tdrainhot - Tdrainout)
Qcold =mcold *Cp *(Tpreheatedout - Tcold)
Now he has made some simplifications in combining the equations Qhot =Qcold , he has deleted Cp from both sides and also used the volumes of water rather than masses. These are ok because we are interested in the ratios, so the conversion from volume to mass would cancel out anyways. He makes the following two mistakes:
- He assumes that Tdrainout = Tpreheatedout, i.e. that the temperature of the drain water leaving the heat exchanger will be the same as the temperature of the preheated water leaving the cold side of the heat exchanger. But there is no reason to assume this. It is like he is pre-solving the problem based on a guess. Without this assumption, and put together correctly, he would end up with one equation and two unknowns, which leaves infinite possible solutions:
Qhot = Qcold
mhot * Cp *(Tdrainhot - Tdrainout) = mcold *Cp * (Tpreheatedout - Tcold)
when we make the cancellations and add the values we know for temperature, we get
75 gallons * (90 - Tdrainout) = 60 * (Tpreheatedout - 55), notice that since Tdrainout does not equal Tpreheatout, we have one equation and two unknowns.
What you end up with is 75/60 * (90 - Tdrainout) = Tpreheatedout -55.
- He does not understand how efficiency is used in the context of a heat exchanger. He is assuming that 80% efficiency means that 80% of the heat lost on the drain side is transferred to the cold water side. He has taken the drain side energy equation Qhot and multiplied by .80 to account for this:
75/60 * .8 (90 - Tdrainout) = Tpreheatedout - 55.
Since 75/60*.8 = 1 the equation works out to:
90 - Tdrainout = Tpreheatedout - 55 which is equivalent to 90 + 55 = Tdrainout + Tpreheatedout, i.e.
145 = Tdrainout + Tpreheatedout
A casual observer will note that this is still one equation with two unknowns, and an infinite number of solutions. We know that Tpreheatedout must be between 55F and 90F, but with the information as presented, we have no idea what Tpreheatedout actually is.
Efficiency in the context of a heat exchanger takes into account how much heat is lost or gained in the first place, and also how much of it is transferred. The engineer has ignored the first part, how much heat is actually lost, hoping to solve this with Qhot = Qcold, which is not possible.
Heat exchanger efficiency is measured through experimentation, and it is referred to as the actual temperature gain (or loss) divided by the total possible temperature gain (or loss).
In this case, the cold water is entering the heat exchanger at 55F, and the drain water is entering at 90F. So the maximum possible outlet temperature on the cold water side is 90F, if the heat exchanger is 100% efficient. The minimum outlet temperature on the cold side is 55, if the efficiency is 0. Any efficiency in between will give a temperature rise in between the two limits.
So Efficiency (e) = (Tpreheatedout - Tcold) / (Tdrainhot - Tcold)
Note also that efficiency on the drain side does not necessarily equal efficiency on the cold side since the flow rates (or volumes) may be different.
When the efficiency is given, as it would be in this type of problem, since it is measured experimentally, it can be used to find the preheated outlet temperature.
This can then be used in the equation Qcold = m Cp dT, to solve for Qcold, which is the energy transferred by the heat exchanger to the cold water. The water heater does not need to heat this water so it energy saved.
This method can be used to solve all of the challenge questions. It is also on our website FAQ section. For natural gas calculations, the energy calculated using this method must be adjusted to account for the lower efficiency of the gas water heater. Electric water heaters have heating elements directly in the cold water. Essentially all of the energy sent to the electric water heater ends up in the water. A gas heater, on the other hand, burns gas, and some of the energy leaves the heater in the form of hot gases. Gas water heaters are rated with an energy factor.
Energy Factor (EF): A measure of water heater overall efficiency, is the ratio of useful energy output from the water heater to the total amount of energy delivered to the water heater. According to Energy Star, new gas water heaters must have an energy factor above 67%. To get btus consumed by a gas water, take btus consumed in an electric water heater and divided by the energy factor.
2 Responses to EcoDrain Payback Calculation Challenge