Building Simple Staircases
I could have easily written a short book on constructing stairs. It is really complicated. I sure wish I could build yours with you side by side. Pay attention because we are going to move quickly.
The first thing I want you to do is to go look at an existing set of stairs. If they were built correctly you can put a straight board down the middle of the steps and each tread nosing (end) will just kiss the board. In other words, the tread nosings are in line.
Check out how each tread is parallel with the tread above and below. The same is true for the risers. Not only that, the intersection of any tread and any riser is a 90 degree angle. The only time this is not true is in a set of concrete or stone steps. The risers in these steps should actually be slanted so that a one inch overhang is created by the slant. See what I mean about complications?
This is The End
A common stumbling block for most beginners is how to determine the cut line for where the stairs begin and end. These lines are very simple. They are just an additional line that is parallel with the risers and treads! Look at your existing stairs and see how this is true.
Calculating Risers and Treads
Just yesterday, I received an email from a builder who is constantly stumped by doing the math for calculating risers. In a perfect world, we would love for these measurements to come out simple fractions or an even amount each time. That is not always the case.
You have to be careful about riser heights. A riser that is too small - say 4 to 5 inches will make a staircase too shallow. A riser over 7.75 inches (current CABO code maximum riser!) can make for a steep staircase. I remember, in the not too distant past, that an 8 inch riser was allowed! Check your local code as an 8 inch riser may be permitted where you live.
Let's pick a random number for the total height distance between two floors. How about 103.5 inches? How can you quickly figure out equal risers for this total rise? Simple! Since I LOVE 7.5 inch risers lets do the math. Divide 103.5 by 7.5......Bummer, the result is 13.8. That means you would have 13 risers at 7.5 inches and the final one would only be .8 of 7.5 inches. I can tell you that this is unacceptable and someone would trip.
The calculation tells us that we NEED 14 risers since we came up with 13.8. So, let's divide 103.5 by 14. the result is 7.3928. This means our risers need to be 7.3928 inches. Well, you won't find that number on a framing square! So how does .3928 inches convert to a fraction on a square? Well the decimal equivalent for 1/8th inch is .125 this means that 3/8 inch is 3 times .125 or .375. So our treads are just a tad over 7 and 3/8 inches. In reality they are actually 7 and 50/128 inches. Heck don't even try to look for 128ths on a framing square! The point is this: See how simple it was to do the math? Always shoot for 7.5 inch risers and then go whatever direction you have to go to make them work out equal keeping in mind your local code's MAXIMUM riser height.
Author's Note: If you need step-by-step color photos of the stair-building process, you should consider my Stair Building eBook. This helpful guide is the answer to all of your frustration over the stair building process. Click the link and you will be amazed at what you will discover.
Stair Building Products
Several companies make some products that will make stair building easier. You will never be able to get away from doing the layout with a framing square but you can eliminate the need for notching stringers or routing grooves for stringers as I always did.
Two companies make simple L shaped metal brackets that you nail to the sides of the stringers. The treads rest on top of these metal brackets. The brackets contain holes on each edge of the L so that you secure the treads and risers. These are very nifty products that allow you to bang together a set of steps in a flash once you have the stringers marked out and cut. the two companies are:
|
Another company makes a triangular wood gizmo that you nail onto stringers. These triangles are adjustable for any tread length and riser height within codes. These create the notched look. You simply nail the treads on top of the triangle blocks.
This product is not meant for outdoor deck steps as the wood brackets are not made from treated lumber. The product comes with easy to follow instructions. Perhaps this is why the product is called EasyRiser!
Call this company for information:
- Building Components Mfg.
800-475-9304
The A, B, C's of Simple Stair Building
Building stairs is a fairly challenging task. It involves mathematics, precision, often difficult measuring, and patience. The concept is fairly straight forward - create treads of equal length and risers of equal height in a given space. However, it confounds many apprentice carpenters! I can only imagine how a homeowner might feel when faced with creating stairs.
The most common stair building errors include:
- First or last riser off by 1 inch or more
- Stair treads not level because of inaccurate total rise measurement
- Top tread depth too shallow because of failure to observe / incorporate top floor nosing depth
90 Degree Angles
Stair building can be simplified if you just learn to trust and understand the relationship of treads / risers/ and a standard framing square. The angle where treads meet risers is simply a 90 degree angle. It just so happens that a standard framing square is permanently set at this angle. How convenient!
Look at Figure 1 for a moment. It is a drawing of a framing square that is resting on the side of a long stair stringer. The tread depth and riser height are not indicated in the drawing. That is OK, because it doesn't make a difference!. No matter what the measurements are, the angle between them (treads and risers) will be maintained at 90 degrees.
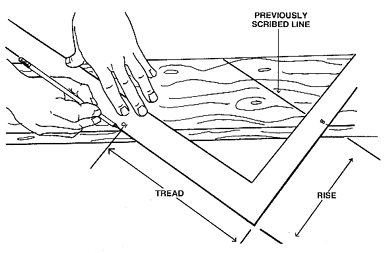
Figure 1
The angle that does change depending upon your situation is the angle of the staircase in relation to the floor lines. If the staircase is steep, then this angle will be greater. For example, if you were crazy and built a staircase with a 12 inch tread and riser, then the angle of the stringer to the floor would be 45 degrees. A more common angle is about 37 degrees. You can achieve this if you build a staircase with a 7.5 inch riser and a 10 inch tread.
You generally don't have to worry about the degrees of this angle? Why? Because the framing square will automatically calculate it for you. Your challenge is to do the math that permits you to create a staircase that gets you as close to the tread and riser limits as set forth in your local building code. I can't quote for you what the standard is, simply because there are different codes across the nation! Here in Cincinnati, we use the CABO One and Two Family Dwelling code. That code stipulates that the ".... maximum riser height shall be 7 and 3/4 inches and the minimum tread depth shall be 10 inches."
Making Things Work Out
To build steps, you have to calculate your total run (the sum of all of the treads) and your total rise (the sum of all of your risers). If you have existing floors you simply measure the distance from floor to floor where the staircase connects at each floor. Failure to do this will goof up your measurements if the floors are not level! You can see how important this is by looking at Figure 2.
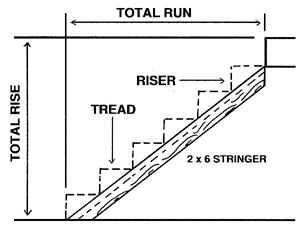
Figure 2
If you are lucky and have no obstructions in front of the staircase where it hits the lower floor, you can let the staircase "run out" some even measurement. For example, choose a 10 or 11 inch tread. Imagine if you will, that the distance between the two floor levels happens to be 112.5 inches. If you choose 7.5 inch risers, this will work perfectly. You end up with 15 risers. Remember, you will always have one less tread than risers. In this case, you end up with 14 treads. So, if you choose the 11 inch tread, the nosing of the lowest tread ends 154 inches away from (14 inches X 11 inches = 154 inches) the top of the staircase opening. To measure your total rise, you need to go out this 154 inches and measure up and back to where the stairs end at the floor above.
The Layout
Look again at Figure 2. See the dashed lines that represent the treads and risers? Perhaps you have seen staircases with notched stringers like this. These notches cut away wood that reduces the weight carrying capability of the staircase. Imagine if you simply slide the dashed lines to the right so that the treads fall within the stringers? That is how we are going to build our staircase. The framing square allows us to do just that.
Look again at Figure 1. Notice how the framing square operator is drawing the second tread line. It is parallel to the first tread line. Note how the framing square rests on the stringer. See the 90 degree relationship between the riser and th tread? The vertical distance once the stringer is in place will be the actual riser height. Thus, the treads and risers are simply a series of parallel lines.
Look, once again, at Figure 1. One of the most confounding tasks is cutting the vertical plumb cut at one end of the stringer, and the flat or bottom seat cut where the stringer rests on the bottom floor. Can you see that these lines are simply a "riser line" and a "phantom" tread? The vertical plumb cut of the staircase is simply a line that is the final riser! The bottom seat cut is simply the top of a tread if your basement floor were another tread in a very long staircase. Are you starting to see that this job is not as hard as it appears at first blush?
Setting The Square on the Stringer
A typical framing square has two different sized legs. Not only are they different lengths, they are different widths. The tongue of a square is the thinner blade (usually 1.5 inches wide) and the body is the 2 inch wide part. The tongue is almost always 16 inches long while the body is 24 inches in length.
For stair construction, you orient the square so that the riser measurement will be on the tongue and the tread on the body. Look at Figure 1. See how the square is placed on the stringer? The 90 degree corner hangs out over the edge. The ruler part of a square always starts at this outside corner and the inch marks proceed each direction out towards the end of each leg. In our previous example (7.5 inch riser and 11 inch treads), you would orient the square so the 7.5 inch mark on the tongue and the 11 inch mark on the body would line up with the long edge of the stringer. ALWAYS use the markings on the same edges of the square. In other words, use the inside rulers of the square or the outside rulers of the square. NEVER mix them up. Don't use the outside ruler on the tongue and the inside ruler of the body!
Start at one end of the stringer, and align the square. If you are using the outside rulers (the method I prefer), then draw a pencil line on the outside edge of the tongue and the body. The tongue pencil marking would be your first riser or the plumb cut, where the string butts against the floor header. The body marking is the top of the first tread. Slide the square down the stringer, until the 7.5 inch marking of the outer edge ruler of the tongue is touching the end of the pencil mark that was created by the body(top of first tread). Align the square so the 11 inch mark of the body is on the edge of the stringer. You have now "stepped" the square down one more riser and tread. Note how the body of the square is parallel with the first tread line you just drew - just as the dashed lines are parallel in Figure 2! Continue making your marks for the rest of your treads & risers. You can do it!
Column B215
8 Responses to Building Simple Staircases